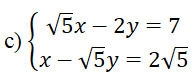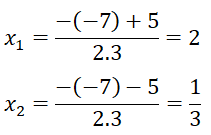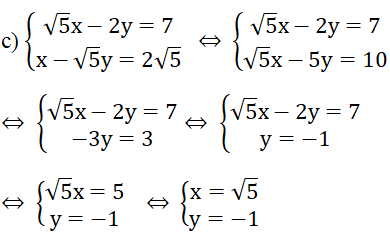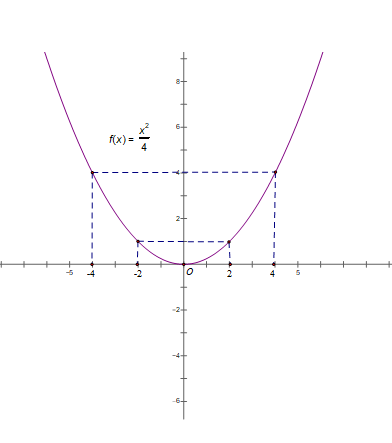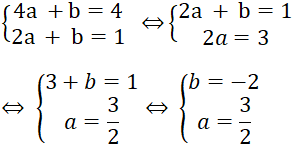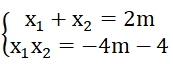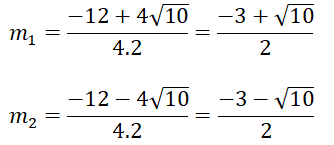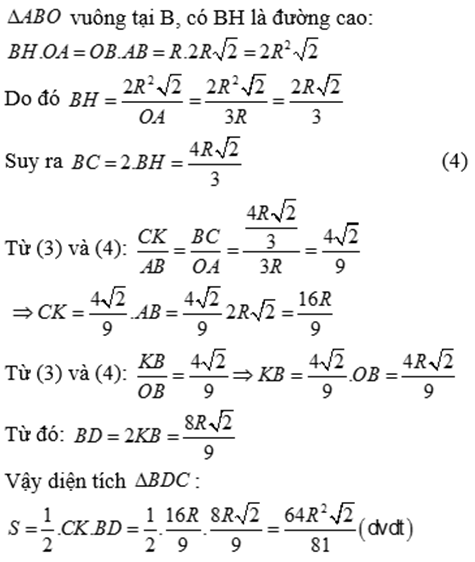Đề thi giữa kì 2 Toán 9 năm 2021 – 2022 mang đến cho các bạn 7 đề kiểm tra có đáp án chi tiết kèm theo bảng ma trận đề thi. Qua đó giúp các bạn có thêm nhiều gợi ý tham khảo, củng cố kiến thức làm quen với cấu trúc đề thi. Hãy cùng tôi tham khảo bài viết dưới đây.
Bài 1 (2,5 điểm)
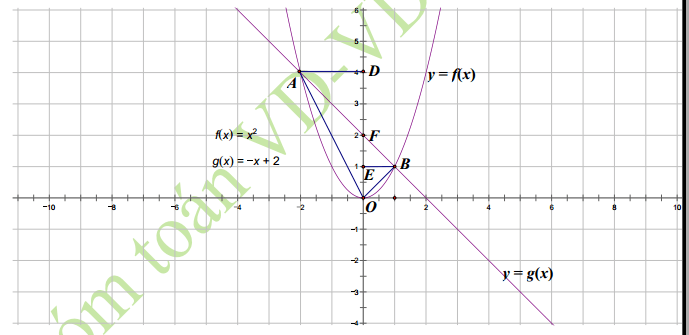
Trong mặt phẳng tọa độ Oxy, cho Parabol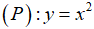 
và đường thẳng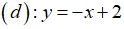 
- Tìm tọa độ giao điểm của (P) và (Q).
- Gọi A, B là hai giao điểm của (P) và (Q). Tính diện tích tam giác OAB,
Bài 2 (2,5 điểm) Giải bài toán bằng cách lập phương trình hoặc hệ phương trình:
Trong tháng đầu, hai tổ sản xuất được 860 chi tiết máy. Đến tháng thứ hai, tổ I vượt mức 15%, tổ II vượt mức 10%. Do đó, tháng thứ hai cả 2 tổ sản xuất được 964 chi tiết máy. Tính số chi tiết máy mỗi tổ đã sản xuất được trong tháng đầu.
Bài 3 (4,0 điểm)
Cho đường tròn tâm O đường kính AB. Dây CD vuông góc với AB tại E (E nằm giữa A và O; E không trùng A, không trùng O). Lấy điểm M thuộc cung nhỏ BC sao cho cung MB nhỏ hơn cung MC. Dây AM cắt CD tại F. Tia BM cắt đường thẳng CD tại K.
- Chứng minh tứ giác BMFE nội tiếp.
- Chứng minh BF vuông góc với AK và EK.EF = EA.EB
- Tiếp tuyến của (O) tại M cắt tia KD tại I. Chứng minh IK = IF.
Bài 4. (1,0 điểm) Với các số a, b, c > 0 và thỏa mãn a + b + c = 1
Chứng minh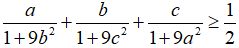 
Đáp án và hướng dẫn giải
Câu 1:
a. Hoành độ giao điểm của (P) và (Q) là nghiệm của phương trình:
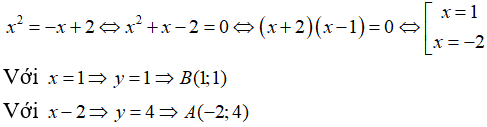
b. Gọi A, B là hai giao điểm của (P) và )Q). Tính diện tích tam giác OAB.
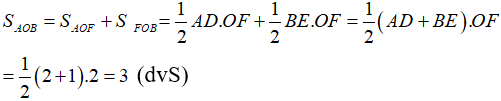
Câu 2:
Gọi số chi tiết máy mỗi tổ đã sản xuất được trong tháng đầu là x, y (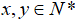
, chi tiết máy)
Vì trong tháng đầu, hai tổ sản xuất được 860 chi tiết máy nên ta có phương trình:
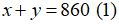
Vì đến tháng thứ hai, tổ I vượt mức 15%, tổ II vượt mức 10%. Do đó, tháng thứ hai cả 2 tổ sản xuất được 964 chi tiết máy, nên ta có phương trình:
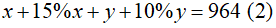
Từ (1) và (2) ta có hệ phương trình:
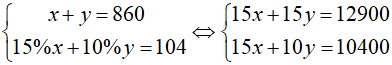
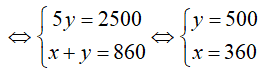
Vậy trong tháng đầu, số chi tiết máy mỗi tổ đã sản xuất được lần lượt là: 360 và 500.
Câu 3:
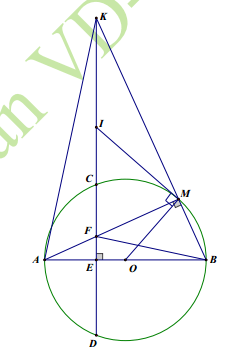
a. Chứng minh tứ giác BMFE nội tiếp.
Ta có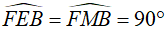 
Nên 4 điểm E, F, M, B cùng thuộc đường tròn đường kính BF, suy ra tứ giác BMFE nội tiếp.
b. Chứng minh BF vuông góc với AK và EK.EF = EA.EB
Nên F là trực tâm, suy ra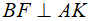 
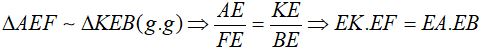
c. Tiếp tuyến của (O) tại M cắt tia KD tại I. Chứng minh IK = IF.
Ta có:
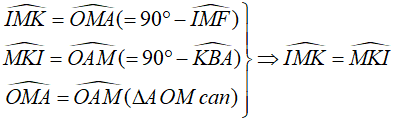
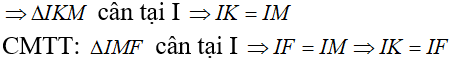
Câu 4:
Ta có:
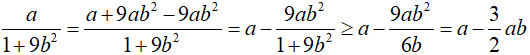
CMTT:
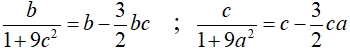
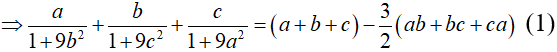
Mặt khác:
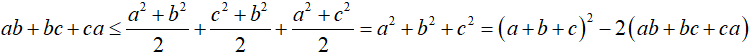
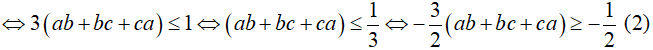
Từ (1) và (2)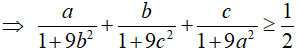 
Dấu “=” xảy ra khi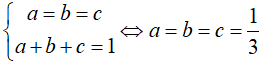 
Phòng Giáo dục và Đào tạo .....
Đề thi Học kì 2
Môn: Toán lớp 9
Thời gian làm bài: 90 phút
Bài 1: (1,5 điểm) Giải các phương trình và hệ phương trình sau:
a) 3x2 – 7x + 2 = 0
b) x4 – 5x + 4 = 0
Bài 2: (1,5 điểm)
a) Vẽ đồ thị (P) hàm số y= x2/4
b) Trên (P) lấy 2 điểm A và B có hoành độ lần lượt là 4 và 2. Viết phương trình đường thẳng đi qua A và B
Bài 3: (1,5 điểm) Cho phương trình (ẩn x) : x2 – 2mx – 4m – 4 = 0(1)
a) Chứng tỏ phương trình (1) có nghiệm với mọi Giá trị của m.
b) Tìm m để phương trình (1) có 2 nghiệm x1, x2 thỏa mãn x12 + x22 - x1x2 = 13
Bài 4: (1 điểm) Tìm kích thước của hình chữ nhật, biết chiều dài hơn chiều rộng 3m. Nếu tăng thêm mỗi chiều thêm 2 mét thì diện tích của hình chữ nhật tăng thêm 70m2.
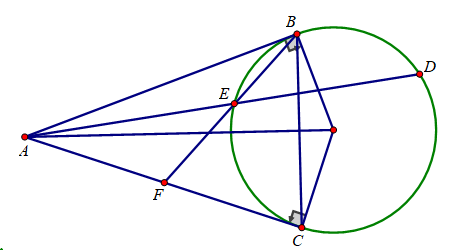
Bài 5: (3,5 điểm) Cho đường tròn (O;R) và một điểm A ngoài đường tròn (O) sao cho OA = 3R. Từ A vẽ hai tiếp tuyến AB, AC với (O) (B, C là các tiếp điểm).
a) Chứng minh tứ giác OBAC nội tiếp và OA vuông góc với BC
b) Từ B vẽ đường thẳng song song với AC cắt đường tròn tâm (O) tại D (D khác B), AD cắt đường tròn (O) tại E (E khác D). Tính tích AD.AE theo R.
c) Tia BE cắt AC tại F. Chứng minh F là trung điểm AC.
d) Tính theo R diện tích tam giác BDC.
Đáp án và Hướng dẫn giải
Bài 1:
a) 3x2 – 7x + 2 = 0
Δ= 72 -4.3.2 = 49 - 24 = 25 > 0 ⇒ √Δ = 5
Phương trình có 2 nghiệm phân biệt:
Vậy tập nghiệm của phương trình là S = {2; 1/3}
b) x4 - 5x2 + 4 = 0
Đặt t = x2 ≥ 0 , ta có phương trình:
t2 - 5t + 4 = 0 (dạng a + b + c = 1 -5 + 4 = 0)
t1 = 1 (nhận) ; t2 = 4 (nhận)
với t = 1 ⇔ x2 = 1 ⇔ x = ± 1
với t = 4 ⇔ x2 = 4 ⇔ x = ± 2
Vậy nghiệm của phương trình x = ±1; x = ± 2
Vậy hệ phương trình có nghiệm (x; y) = ( √5; -1)
Bài 2:
a) Tập xác định của hàm số: R
Bảng giá trị:
| x | -4 | -2 | 0 | 2 | 4 |
| y = x2 / 4 | 4 | 1 | 0 | 1 | 4 |
Đồ thị hàm số y = x2 / 4 là một đường parabol nằm phía trên trục hoành, nhận trục Oy làm trục đối xứng và điểm O(0;0) là đỉnh và là điểm thấp nhất.
b) Với x = 4, ta có: y = x2/4 = 4 ⇒ A (4; 4)
Với x = 2, ta có y = x2/4 = 1 ⇒ B ( 2; 1)
Giả sử đường thẳng đi qua 2 điểm A, B là y = ax + b
Đường thẳng đi qua A (4; 4) nên 4 = 4a + b
Đường thẳng đi qua B (2; 1) nên : 1= 2a + b
Ta có hệ phương trình
Vậy phương trình đường thẳng đi qua 2 điểm A, B là y = 3/2 x - 2
Bài 3:
a) Δ' = m2 - (-4m - 4) = m2 + 4m + 4 = (m + 2)2 ≥ 0 ∀m
Vậy phương trình đã cho luôn có nghiệm với mọi m
b) Gọi x1 ; x2 lần lượt là 2 nghiệm của phương trình đã cho
Theo hệ thức Vi-et ta có:
x12 + x22 -x1 x2 = (x1 + x2 )2 - 3x1 x2 = 4m2 + 3(4m + 4)
Theo bài ra: x12 + x22 - x1 x2=13
⇒ 4m2 + 3(4m + 4) = 13 ⇔ 4m2 + 12m - 1 = 0
Δm = 122 -4.4.(-1) = 160 ⇒ √(Δm ) = 4√10
Phương trình có 2 nghiệm phân biệt
Vậy với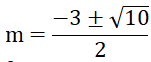 
thì phương trình có 2 nghiệm x1; x2 thỏa mãn điều kiện x12 + x22 - x1 x2 = 13
Bài 4:
Gọi chiều rộng của hình chữ nhật là x (m) ( x > 0 )
⇒ Chiều dài của hình chữ nhật là x + 3 (m)
Khi đó diện tích của hình chữ nhật là x(x + 3) (m2 )
Nếu tăng thêm mỗi chiều thêm 2 mét thì diện tích của hình chữ nhật tăng thêm 70m2 nên ta có phương trình:
(x + 2)(x + 3 + 2) = x(x + 3) + 70
⇔ (x + 2)(x + 5) = x(x + 3) + 70
⇔ x2 + 7x + 10 = x2 + 3x + 70
⇔ 4x = 60
⇔ x = 15
Vậy chiều rộng của hình chữ nhật là 15m
Chiều dài của hình chữ nhật là 18m
Bài 5:
👉 Trên đây, tôi đã giới thiệu tới các bạn Đề thi Toán lớp 9 học kì 2 năm 2021 có đáp án. Ngoài ra, các bạn có thể tham khảo thêm các tài liệu lớp 9 khác như: Giải bài tập Toán lớp 9, Giải Vở BT Toán 7 và các dạng Đề thi học kì 2 lớp 9 ... Chúc các bạn thi tốt.
